Your feedback on these self-help problems is appreciated. Click here to send an e-mail.

For on-line tutorial help with kinetics, there are four modules available in the Kinetics section of chemcal.

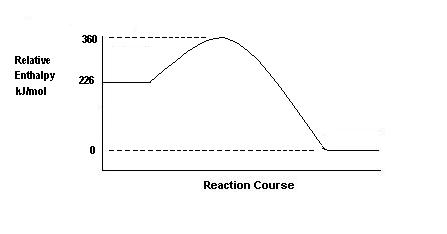
What is the meaning of E_A on the diagram?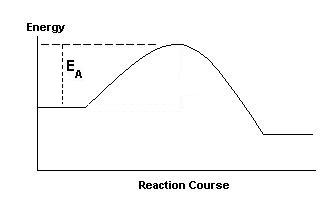

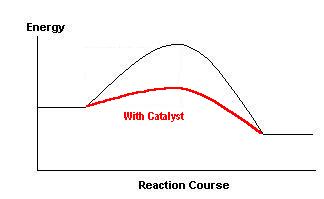
(b) Indicate on the diagram the effect of the presence of a catalyst.

CO(g) + NO₂(g) → CO₂(g) + NO(g)

(a) What is the activation energy for the reaction?
(b) What is the activation energy for the reverse reaction?
(c) What is the value of ΔH for the reaction?
(d) Explain briefly the effect of an increase in temperature on the rate of the forward reaction.

2NO₂^- + 2I^- + 4H⁺ → I₂ + 2NO + 2H₂O

The experimental rate law for this reaction is
R = k[NO₂^-][I^-][H⁺]²
By what factor, if any, would the rate of reaction be altered if-

(a) [H⁺] and [I^-] were kept constant but [NO₂^-] were doubled?
(b) [I^-] and [NO₂^-] were kept constant but [H⁺] were doubled?
(c) [I^-] and [NO₂^-] were kept constant but [H⁺] were halved?
(d) All concentrations were doubled?

R = k[H₃O⁺][NH₃]

where k = 4.3 x 10¹⁰ litre mole^-1 second^-1 at 298 K.  Calculate the rate of this acid-base reaction the instant 0.10 M ammonia (400 cm³) is mixed with 0.050 M nitric acid (200 cm³).

(b) The effect of the catalyst is to lower the height of the "hump". By offering a new route the presence of the catalyst lowers E_A (for both forward and backward reactions).

(a) From the graph, E_A for the forward reaction = (360 - 226)

= 134 kilojoule mole^-1

(b) From the graph, E_A for the reverse reaction = (360 - 0)

= 360 kilojoule mole^-1

(c) The enthalpy change, ΔH = (0 - 226) = -226 kilojoule mole^-1

(d) At higher temperatures the proportion of molecules with the necessary activation energy is increased. Rate of forward (and backward) reaction is thus increased.

Note that unlike equilibrium constants, a rate law expression cannot be deduced from the stoichiometric equation. Instead it requires a series of separate experiments to deduce in turn the effect that the concentration of each reactant has on the overall rate of the reaction. In a series of experiments, only one reactant's concentration is altered in each experiment while the concentrations of all the other reactants are held unchanged. By these means, the effect of changing the concentration of each reactant in turn on the rate of the overall reaction can be determined.
In the first experiment, doubling the concentration of A (written as [A]) alone doubles the rate of formation of E, so the reaction rate is directly proportional to [A].
i.e. rate = constant x [A]¹.
In the second experiment, keeping [A] and [C] fixed while doubling [B] alone causes the rate of formation of E to double, so the reaction rate is directly proportional to [B] as well.
i.e. rate= constant x [B]¹.
In the third experiment to establish the effect of changing the concentration of C alone, the rate of the reaction is not altered so [C] does not appear in the rate law for the reaction,
or rate = constant x [C]⁰.
Combining these results,
rate = k[A]¹[B]¹[C]⁰ , or rate = k[A][B]

In this question, the rate law is not requested and in fact the data needed to deduce it is not given. Here the simple stoichiometric relationship between the various reactants and products is all that is required to establish their relative rates of consumption or formation. In general terms, suppose that 1 molecule of a reactant A uses 2 molecules of another reactant B to form 1 molecule of product C, then the rate of consumption of B is twice that of A and that the rate of formation of C is identical to the rate of consumption of A.

In this question, 2 molecules of NO reacts with 1 molecule of O₂ so the rate of consumption of NO must be twice that of O₂ while each molecule of NO forms 1 molecule of NO₂, so the rate of consumption of NO is the same as the rate of formation of NO₂.

By convention, the consumption of a reactant is shown by attaching a negative sign to its rate while the formation of a product is indicated by a + sign associated with its rate.

In words, the rate of consumption of NO equals the rate of formation of NO₂, and the rate of disappearance of O₂ is one-half this rate.

Or, using the calculus notation of d[A]/dt for the rate of change of concentration of any species A,

2 x -d[NO]/dt = -d[O₂]/dt = + 2 x d[NO₂]/dt

(b) If only the [H⁺] is altered and is doubled, then from the rate law, this would cause the rate to increase by a factor of 4 as rate ∝ [H⁺]².

(c) If only the [H⁺] is altered and is halved, then from the rate law, this would cause the rate to decrease to ¼ of the original rate as rate ∝ [H⁺]², i.e. ( ½. )² = ¼.

(d)   If all concentrations were doubled, then the doubling of [NO₂^-] would double the rate and doubling the [I^-] would double the rate again (now increased by a factor of 4) and doubling the [H⁺] would increase the rate by a further factor of 4 to give a total increase in rate of 16 times the original rate.

The rate law is rate = 4.3 x 10¹⁰ [H₃O⁺][NH₃].

Calculate the instantaneous [H₃O⁺] and [NH₃] which have been diluted upon mixing as follows:

Total volume.= 600 mL.

For dilutions, the expression M₁V₁ = M₂V₂ is valid.

so [H₃O⁺] = 1.67 x 10^-2 M

and for the diluted [NH₃], 0.10 x 400 = M₂ x 600

so [NH₃] = 6.66 x 10^-2 M

Substituting these values for [H₃O⁺] and [NH₃] in the rate law

Rate = 4.3 x 10¹⁰ [H₃O⁺][NH₃]

         = 4.3 x 10¹⁰ (1.67 x 10^-2)(6.66 x 10^-2)

          = 4.8 moles litre^-1 second^-1  (4.8 M s^-1)

     ∴ rate is directly proportional to the [C₆H₅N₂Cl], so n = 1.

(b)   Substitute either set of data in the rate equation.

 8.70 x 10^-7 = k x 0.0200

∴ k = 4.35 x 10^-5 s^-1.

(c)   See answer to Question 4 above for a discussion of the background to this part.

From the stoichiometry of the equation, each mole of C₆H₅OH produced corresponds to the consumption of one mole of C₆H₅N₂Cl. Hence an alternative differential expression for the rate would be

-d [C₆H₅N₂Cl] /dt      (The - sign indicates that species is being consumed)

The relation between them is

(b)   As n = 1, reaction order = 1.

(c) To evaluate k, substitute any of the sets of data.

0.10 = k x 0.340

∴ k = 2.9 x 10^-1 hr^-1.