
In infrared spectroscopy, transitions are allowed between adjacent v levels for a harmonic oscillator - the selection rule is:
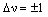
where an increase in v corresponds to absorption and a decrease in v corresponds to emission. Anharmonicity changes this rule, allowing v to change by any value:
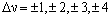
Absorption corresponding to Dv = 1 is by far the most probable and, as v = 0 is the most populated level, the transition corresponding to v = 0 to v = 1 leads to the strongest band, called the fundamental frequency. The additional transitions with larger Dv are called overtones and are usually very weak and get increasingly weak as Dv increases.
The transition energy is the difference in energy between the vibrational levels. If one level has vibrational quantum number v then the strongest absorption is to the level with quantum number (v+1). The energy of these levels is:
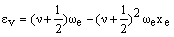
and
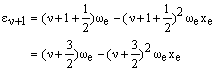
The energy difference is then:
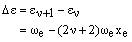
The most populated vibrational level has v = 0 leading to a transition frequency for the fundamental of:
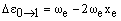
The vibrational levels with v = 1, 2, 3... have rapidly decreasing populations. If observed at all, their transition frequencies will be:
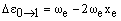
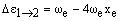
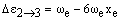
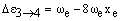
respectively. As xe is small and positive, these transitions occur at slightly lower frequency than the fundamental. Due to the low populations of these levels, the bands are extremely weak. However, increasing the temperature increases the populations and so the band intensities grow. For this reason, they are called hot bands and are usually detected in this way. As noted above, weak overtones may occur from larger changes in v. From the v = 0 level, the first few overtones have frequencies:
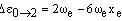
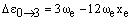
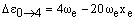
The overtones have frequencies which are almost multiples of the fundamental but, due to the small positive value of xe, have slightly lower frequency.
Input values into the calculator below for the force constant, atomic masses and dissociation energy and press "calculate" to work out the energy levels and transition energies. Input a value for the temperature to work out the relative intensity of each transition.
Once you have covered all of the available resources for vibrational
spectroscopy, you should test your knowledge and understanding with the self test.
Hit the 'Graphical' button to see the predicted spectrum and an interactive graphical version of this calculator.
|
