Real molecules do not behave like Hooke's springs. A Hooke's spring will restore to its equilibrium separation however much it is stretch whereas a real bond will eventually break. When the bond breaks, there is no longer a restoring force and the separation can be increased without further changing the energy. Similarly, if a real bond is compressed too much, the atomic cores start to overlap and there is a rapid increase in electron-electron and nucleus-nucleus repulsion and so the energy rapidly increases.
A purely empirical expression that fits this behaviour is the Morse function:
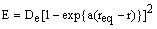
where De is the bond dissociation energy, req is the equilibrium bond length and a is a constant for a particular molecule. Using this function, the quantum mechanical energy levels (in cm-1) are:
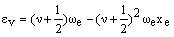
where we is the anharmonic oscillation frequency (see below) and xe is the anharmonicity constant (which is small and positive). In the harmonic case, the vibrational levels are equally spaced. The second term in the anharmonic equation causes the levels to become more closely spaced as v increases. At high v values, the energy levels converge to the dissociation energy.
This equation can be rewritten in a form which can be compared with that for the harmonic oscillator:
harmonic |
|
anharmonic |
| |
|
|
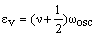 |
|
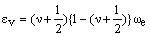 |
which suggests that:
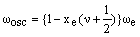
As xe is positive, anharmonic oscillation frequency we is greater than wosc and the anharmonic oscillator behaves like the harmonic oscillator but wosc decreases with increasing v. For the hypothetical state with v = -1/2 corresponding to the bottom of the energy well when the vibrational energy would be zero, we = wosc. The dissociation energy is related to the wosc and xe:
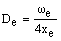
Input values into the calculator below for the force constant and atomic masses and press "calculate"
to work out the energy levels.
The number of molecule in an energy level (Nv, compared to the number in the lowest level (N0 = 0) is given by the Boltzmann distribution:
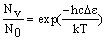
where De is the difference in energy between the level and the lowest possible level (v = 0). Input a temperature into the calculator and press "calculate" to work out the populations.
Once you have covered all of the available resources for vibrational
spectroscopy, you should test your knowledge and understanding with the self test.
Hit the 'Graphical' button to see an interactive graphical version of this calculator.
