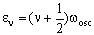
where v is the vibrational quantum number which can be zero or any positive integer (0, 1, 2, 3, 4, 5....). w_osc is the oscillation frequency. The allowed energies form 'a ladder' of equally spaced levels. Classically, this is given (in cm^-1) as:

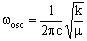
where c is the speed of light (2.998 x 10^-10 cm s^-1), k is the bond 'force constant' and m is the reduced mass. The force constant is related to the 'stiffness' of the bond so that a stronger bond will have a larger force constant than a weaker bond. The reduced mass is simply related to the masses of the two atoms (m₁ and m₂):

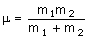
Input values into the calculator below for the force constant and atomic masses and press "calculate" to work out the energy levels.

The number of molecule in an energy level (N_v), compared to the number in the lowest level (N₀) is given by the Boltzmann distribution:

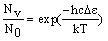
where De is the difference in energy between the level and the lowest possible level (v = 0). Input a temperature into the calculator and press "calculate" to work out the populations.

Once you have covered all of the available resources for vibrational spectroscopy, you should test your knowledge and understanding with the self test.

Hit the 'Graphical' button to see an interactive graphical version of this calculator.