Molecules simultaneously rotate and vibrate. The energy of a vibrating, rotating molecule is given by adding the equations for these two contributions:
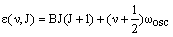
where the energies (in cm-1) are for the rigid-rotor, harmonic diatomic for simplicity. J is the rotational quantum number and be zero or any positive integer (0, 1, 2, 3, 4, 5...). v is the vibrational quantum number and can also be zero or any positive integer. wosc is the harmonic frequency. B is the rotational constant and is inversely proportional to the moment of inertia of the molecule, I:
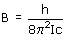
where h is Planck's constant (6.626 x 10-34 J s) and c is the speed of light (2.998 x 10-10 cm s-1). The moment of inertia for a diatomic molecule is simply related to the length of the bond (r) and the masses of the two atoms (m1 and m2):
|
|
where m is the reduced mass, given by |
|
|
The value of B therefore depends on r2 and this varies, even in the harmonic case, with the vibrational level. As the amplitude of the vibration increases with increasing vibrational energy, r2 increases leading to a decrease in B. If Be is the value of the rotational constant at the equilibrium bond length (the bottom of the energy well), then this dependence on the vibrational level is normally expressed as:
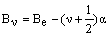
where a is a small, positive constant.
Input values into the calculator below for the bond length, atomic masses, vibrational frequency and a and press "calculate" to work out the energy levels. Alternatively, just enter values for the rotational constants to work out the energy levels.
The population of the levels depends on their overall energies and are, as for the pure rotational case, also dependent on the (2J+1) degeneracy of each rotational level. Input a value for the temperature and press "calculate" to work out the populations.
Once you have covered all of the available resources for vibrational
spectroscopy, you should test your knowledge and understanding with the self test.
Hit the 'Graphical' button to see an interactive graphical version of this calculator.
