 |
Rovibrational Spectrum For A Rigid-Rotor Harmonic Diatomic Molecule |
| | |
| |

For most diatomic molecules, vibrational transitions must* be accompanied by a simultaneous change in the rotational energy.
If the lower vibrational state has vibrational quantum number v and rotational quantum number J and the upper vibrational level has vibrational quantum number v' and rotational quantum number J', their rovibrational energies are respectively:
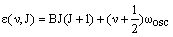
and
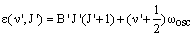
Separate rotational constants, B'' and B', have been given as these are likely to be very different in the two vibrational levels - the rotational constant depends sensitively on the bond length.
For a harmonic oscillator, transitions are allowed between adjacent v levels - the selection rule is:
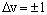
For most* diatomic molecules,
simultaneous change in the rotational energy occurs with the selection rule:
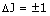
Many of the rotational levels are likely to be populated at normal temperatures and two series or branches of lines result from:
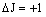 | R branch |
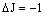 | P branch |
R branch
The R branch corresponds to simultaneous excitation of vibrational and rotational energy, so v' = v + 1 and J' = J + 1. The energy difference is then:
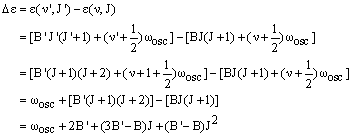 |
(1) |
In the case where B = B', this becomes:

The first member of the series, denoted R(0), has J = 0 and a transition energy which is greater than the pure vibrational energy by 2B'. In the case where B' = B, there are a series of lines from J = 1, 2, 3 ..., denoted R(1), R(2), R(3) ..., which are separated from this by 2B - just as in the pure rotational spectrum. Real molecules have B' < B so that the (B'-B)J2 in equation (1) is negative and gets larger in magnitude as J increases. The result is that the separation of the lines in the R-branch tend to decrease with J.
P branch
The P branch corresponds to vibrational excitation and reduction in the rotational energy, so v' = v + 1 and J' = J - 1. The energy difference is then:
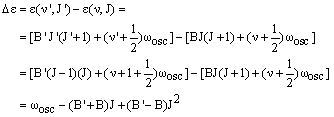 |
(2) |
In the case where B = B', this becomes:
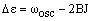
The first member of the series, denoted P(1), has J = 1 (a transition from J = 0 and J' = J - 1 is not possible). Its transition energy is lower than the pure vibrational energy by (B'+B). In the case where B' = B, this is 2B and there are a series of lines from J = 2, 3, 4 ..., denoted P(2), P(3), P(4) ..., which are separated from this by 2B - just as in the pure rotational spectrum. Real molecules have B' < B so that the (B'-B)J2 in equation (2) is negative and gets larger in magnitude as J increases. This leads to lines with even lower energies whose separation increases with J.
Q branch
Diatomic molecules with a degenerate electronic ground state also show transitions with no change in rotational quantum number so that J' = J. The most common diatomic molecules in this class are those with an odd number of unpaired electrons with nitrogen monoxoide (NO) being the most common.
This gives rise to an extra set of transitions called the Q branch.
The Q branch corresponds to vibrational excitation with no change in the rotational quantum number, so v' = v + 1 and J' = J - 1. The energy difference is then:
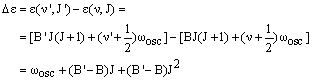 |
(3) |
In the case where B = B', this becomes:
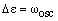
In this case, each transition in the Q branch (from every rotational level of the lower vibrational state) occurs at the same frequency - the energy of the pure vibrational transition! This results in a high intensity line between the P and R branches.
If B' < B, (B'-B) is negative and the transitions are displaced from this position to lower energy by an amount that increases with J. The first member of the series, denoted Q(1), has J = 0 and a transition energy equal to the pure vibrational energy. The series of lines from J = 1, 2, 3 ..., denoted Q(1), Q(2), Q(3) ..., are to lower and lower energy and with separation that increases with J.
The intensity of each line in the P, Q and R branches depends on the population and energy of the rotational levels in a very similar way to that for the pure rotational spectrum.
Once you have covered all of the available resources for vibrational
spectroscopy, you should test your knowledge and understanding with the self test.
Hit the 'Graphical' button to see an interactive graphical version of this calculator.
|
|
|
