A
chemical equation describes what happens when a chemical reaction takes place. It uses chemical formulae to tell us what happens when the
reactants (left) react to form the
products.
d
For example, when methane burns in air, the reactants are
CH4(g) (methane) and
O2(g) (oxygen in the air). The products are
CO2(g) (carbon dioxide) and
H2O(g) (water). An arrow meaning
react to produce is used to show the process:
CH4(g) + O2(g) → CO2(g) + 2H2O(l)
The arrow tells us that methane and oxygen react to form carbon dioxide and water. The reverse reaction, in which carbon dioxide and water react to form methane and oxygen does not occur so the arrow only points from left to right. Some reactions, however, can go either way. For example,
N2(g) (nitrogen) and
H2(g) (hydrogen) react to form
NH3(g) (ammonia). However
NH3(g) will also react with itself to form
N2(g) and
H2(g). Such reactions are said to be
reversible. This is represented by either a double headed arrow, ↔, or the equilibrium arrow, ⇌:
| N2(g) + 3H2(g) ↔ 2NH3(g) or |
| N2(g) + 3H2(g) | 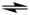 | 2NH3(g) |
Stoichiometry (pronounced
"stoi-kee-om-i-tree",) is concerned with the relative amounts of reactants and products in a reaction. In the reaction of nitrogen and hydrogen to produce ammonia, the chemical equation has a number 3 in front of H
2(g) and a number 2 in front of NH
3(g). These are the
stoichiometric coefficients and they indicate the number of molecules or moles of each kind among the reactants and products. When no number is written, as for N
2(g), then the stoichiometric coefficient is 1. The chemical equations above thus should be read to mean:
-
CH4(g) + O2(g) → CO2(g) + 2H2O(l):
"1 molecule of methane reacts with 1 molecule of oxygen to make 1 molecule of carbon dioxide and 2 molecules of water", or
"1 mole of methane reacts with 1 mole of oxygen to make 1 mole of carbon dioxide and 2 moles of water".
-
N2(g) + 3H2(g) ↔ 2NH3(g):
"1 molecule of nitrogen reacts with 3 molecules of hydrogen to produce 2 molecules of ammonia", or
"1 mole of nitrogen reacts with 3 moles of hydrogen to produce 2 moles of ammonia".
The coefficients are chosen to ensure that the 'law of conservation of mass' is observed: because atoms are not created or destroyed during a reaction, there must be the same number of each sort on both sides of the arrow. Choosing the coefficients is called
balancing the chemical equations and is really just a bookkeeping or exercise in accountancy applied to chemistry. There are many ways of approaching what is essentially just a logic puzzle. The following is a set of tactics that may help.
Write the reactants on the left, with plus signs between them, and the products on the right, with plus signs between them. Join the two sides with an arrow. Make sure the formulae are correct and the states (s, l, g or aq) are included!
Follow the steps in order - keep checking the tally as you can stop as soon as it is balanced!
- Tally up the number of each atom on both sides on your unbalanced equation.
- Balance metallic atoms.
- Balance polyatomic ions or groups (like SO42-, NO3- etc) that appear unchanged on both sides of the equation.
- Balance any remaining non-metallic atoms and, of these, balance H and O last.
- Balance elemental substances (such as O2(g), H2, Al(s) etc) last.
- Divide the coefficients through to give the smallest whole numbers.
Example 1:
| |
Reactants |
|
|
|
Products |
|
Balanced? |
|
|---|
| 1. |
N2(g) + H2(g) |
|
→ |
|
NH3(g) |
|---|
|
2 × N
2 × H |
|
|
|
1 × N
3 × H |
|
No |
|---|
| 2. |
No metal atoms involved |
|---|
| 3. |
All groups change |
|---|
| 4. | There are 2N on the left so we put a 2 in front of NH3 on the right to balance N.
|
|---|
|
N2(g) + H2(g) |
|
→ |
|
2NH3(g) |
|---|
|
2 × N
2 × H |
|
|
|
2 × N
6 × H |
|
No |
|---|
| 5. | There are now 6H on the right so we put a 3 in front of H2 on the left to balance N.
|
|---|
|
N2(g) + 3H2(g) |
|
→ |
|
2NH3(g) |
|---|
|
2 × N
3 × 2 = 6 × H |
|
|
|
2 × N
6 × H |
|
Yes |
|---|
| 6. | The coefficients (1, 3 and 2) are already the smallest whole numbers that are possible. The job is done.
|
|---|
|
Example 2:
| |
Reactants |
|
|
|
Products |
|
Balanced? |
|
|---|
| 1. |
Al(s) + H2SO4(aq) |
|
→ |
|
Al2(SO4)3(aq) + H2(g) |
| | |
|---|
|
1 × Al
2 × H
1 × S
4 × O |
|
|
|
2 × Al
2 × H
3 × S
3 × 4 × O* = 12 × O |
|
No |
|---|
| Note that Al2(SO4)3 contains 2Al, 3S and 12O. The brackets around SO4 mean that the 3 outside the bracket refers to everything inside the brackets, just as in a maths equation. |
| |
| 2. | There is 1Al on the left and 2Al on the right so we put a 2 in front of Al(s) on the left to balance Al. |
|---|
| 2Al(s) + H2SO4(aq) |
|
→ |
|
Al2(SO4)3(aq) + H2(g) |
| | |
|---|
|
2 × Al
2 × H
1 × S
4 × O |
|
|
|
2 × Al
2 × H
3 × S
12 × O |
|
No |
|---|
| 3. | The SO4 group is unchanged in the reaction. There are 3 (SO4) groups on the right and only 1 on the left, so we put a 3 in front of H2SO4(aq) on the left. |
|---|
| 2Al(s) + 3H2SO4(aq) |
|
→ |
|
Al2(SO4)3(aq) + H2(g) |
| | |
|---|
|
2 × Al
3 × 2 × H = 6 × H
3 × S
3 × 4 × O = 12 × O |
|
|
|
2 × Al
2 × H
3 × S
12 × O |
|
No |
|---|
| 4. | Everything is balanced except H. |
|---|
| 5. | There are 6 H on the left and only 2 H on the right so we put a 3 in front of H2(g) on the right: |
|---|
| 2Al(s) + 3H2SO4(aq) |
|
→ |
|
Al2(SO4)3(aq) + 3H2(g) |
| | |
|---|
|
2 × Al
6 × H
3 × S
12 × O |
|
|
|
2 × Al
3 × 2 = 6 × H
3 × S
12 × O |
|
Yes |
|---|
| 6. | The coefficients (2, 3, 2 and 3) are already the smallest whole numbers that are possible. The job is done.
|
|---|
|
Example 3:
| |
Reactants |
|
|
|
Products |
|
Balanced? |
|
|---|
| 1. |
C2H5OH(l) + O2(g) |
|
→ |
|
CO2(g) + H2O(l) |
| | |
|---|
|
2 × C
5 × H + 1 × H = 6 × H
1 × O (from C2H5OH) +
2 × O (from O2) = 3 × O |
|
|
|
1 × C
2 × H
2 × O (from CO2) +
1 × O (from H2) = 3 × O |
|
No |
|---|
| 2. |
No metal atoms involved |
|---|
| 3. |
All groups change |
|---|
| 4. |
There are 2 C on the left and only 1 C on the right so we put a 2 in front of CO2 on the right |
|---|
| C2H5OH(l) + O2(g) |
|
→ |
|
2CO2(g) + H2O(l) |
| | |
|---|
|
2 × C
6 × H
3 × O |
|
|
|
2 × C
2 × H
2 × 2 × O (from CO2) +
1 × O (from H2) = 5 × O |
|
No |
|---|
|
There are 6 H on the left and only 2 H on the right so we put a 3 in front of H2O on the right |
|---|
| C2H5OH(l) + O2(g) |
|
→ |
|
2CO2(g) + 3H2O(l) |
| | |
|---|
|
2 × C
6 × H
3 × O |
|
|
|
2 × C
3 × 2 × H = 6 × H
4 × O (from CO2) +
3 × O (from H2O) =
7 × O |
|
No |
|---|
| 5. | Everything is balanced except O. There are 3 O on the left: 1 × O from C2H5OH and 2 × O from O2(g). There are 7 O on the right. Multiplying C2H5OH by a number would change C and H but multiplying O2 only affects O. This is why elements are left to the end. We put a 3 in front of O2: |
|---|
| C2H5OH(l) + 3O2(g) |
|
→ |
|
2CO2(g) + 3H2O(l) |
| | |
|---|
|
2 × C
6 × H
1 × O (from C2H5OH) +
3 × 2 × O (from O2) =
7 × O |
|
|
|
2 × C
6 × H
7 × O |
|
Yes |
|---|
| 6. | The coefficients (1, 3, 2 and 3) are already the smallest whole numbers that are possible. The job is done.
|
|---|
|
Example 4:
| |
Reactants |
|
|
|
Products |
|
Balanced? |
|
|---|
| 1. |
C30H62(s) + O2(g) |
|
→ |
|
CO2(g) + H2O(l) |
| | |
|---|
|
30 × C
62 × H
2 × O |
|
|
|
1 × C
2 × H
2 × O (from CO2) +
1 × O (from H2) = 3 × O |
|
No |
|---|
| 2. |
No metal atoms involved |
|---|
| 3. |
All groups change |
|---|
| 4. |
There are 30 C on the left and only 1 C on the right so we put a 30 in front of CO2 on the right |
|---|
| C30H62(s) + O2(g) |
|
→ |
|
30CO2(g) + H2O(l) |
| | |
|---|
|
30 × C
62 × H
2 × O |
|
|
|
30 × C
2 × H
30 × 2 × O (from CO2) +
1 × O (from H2O)
= 61 × O |
|
No |
|---|
| 4. |
There are 62 H on the left and only 2 H on the right so we put a 31 in front of H2O on the right |
|---|
| C30H62(s) + O2(g) |
|
→ |
|
30CO2(g) + 31H2O(l) |
| | |
|---|
|
30 × C
62 × H
2 × O |
|
|
|
30 × C
31 × 2 × H = 62 × H
30 × 2 × O (from CO2) +
31 × 1 × O (from H2O) = 91 × O |
|
No |
|---|
| 5. | Everything is balanced except O. There are 2 O on the left and 91 O on the right. Multiplying O2 by 91/2 leads to the cumbersome looking: |
|---|
| C30H62(s) + 91/2O2(g) |
|
→ |
|
30CO2(g)(s) + 31H2O(l) |
| | |
|---|
|
30 × C
62 × H
91/2 × 2 × O = 91 × O |
|
|
|
30 × C
62 × H
91 × O |
|
Yes |
|---|
| 6. | This looks strange but as O is only in O2 on the left, it was the easiest thing to do. We can now multiply all of the coefficients by 2 to give the final balanced equation: |
|---|
| 2C30H62(s) + 91O2(g) |
|
→ |
|
60CO2(g) + 62H2O(l) |
| | |
|---|
|
2 × 30 × C = 60 × C
2 × 62 × H = 124 × H
91 × 2 × O = 182 × O |
|
|
|
60 × C
62 × 2 × H = 124 × H
60 × 2 × O (from CO2)
+ 62 × O (from H2O)
= 182 × O |
|
Yes |
|---|
|
Each quiz is made up of 10 questions randomly drawn from a large set so you can repeat the quiz many times over. The results are not stored!
Practice multiple choice questions (not an assessment)