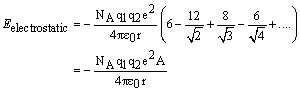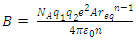1 Introduction
In this experiment, the structures of many elements and compounds are rationalized using simple packing models. The pre-work revises and extends the material presented in the lecture course.
2 The Lattice Energy of Ionic Compounds
The compounds formed between elements of very different electronegativities are usually ionic in character. Ionic compounds are usually solids at room temperature, although ionic liquids also exist. They are held together in three-dimensional arrangements by the attractive forces between every pair of oppositely charged ions – not just by the interaction between neighbouring ions. The energy that is required to completely separate the ions is called the lattice energy.
| The unit cell for the rocksalt structure of NaCl is shown opposite. The structure can be rotated with the mouse. The unit cell is the simplest structure that generates the whole lattice when repeated infinitely in all directions.
The distance between the ions is determined by the balance of the attractive force between cation and anion and the repulsive forces between both the core electrons of the ions and their nuclei.
The simplest model imagines that the ions are hard spheres with fixed radii. The ions touch but do not overlap. We first use this model to calculate the lattice energy and then show how the model is improved by including the compressibility of the ions.
If the charges on the cation and anion are q1 and q2, the attractive interaction between a pair is:
where e is the charge on an electron, ε0 is the permittivity of a vacuum and r is the distance between the centres of the ions. |
|
In the sodium chloride structure, the Na+ ion at the centre is surrounded by six Cl- at a distance r. The attractive potential energy is:
|
| (1) |
The next nearest neighbours for the Na+ ion are the twelve Na+ ions on each edge of the unit cell, at a distance of (2)1/2r. This gives rise to a repulsive potential energy term:
|
| (2) |
In the next shell, the Na+ ion experiences an attractive potential energy with the eight Cl- ions at the corner of the unit cell, at a distance of (3)1/2r:
|
| (3) |
The net attractive energy between the Na+ ion and all other ions in the crystal is given by the infinite (and slowly converging series):
|
| (4) |
This summation is repeated for every ion in the crystal (i.e. 2NA ions per mole of NaCl). As this counts every interaction twice, it is then necessary to divide by two giving the total energy as:
|
| (5) |
where the Madelung Constant, A, is the numerical value of the infinite series summation. The Madelung constant depends only on the crystal structure not on the size or charge of the ions. Every compound with the rocksalt structure has the same Madelung constant. The table below lists the Madelung constant for a number of common structural types.
Table 1. The Madelung constant for common MX and MX2 structures. The final column shows the Madelung constant divided by the number of ions in the chemical formula.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Note that, for a given stoichiometry, the Madelung constant and, hence, the lattice energy, increase with the coordination number:
Solids adopt structures with higher coordination numbers to maximize the ionic bonding
One curious feature of the expression in equation (5) is that the lattice energy has the largest magnitude when r = 0! The model does not implicitly include any repulsion between unlike charges. The hard sphere model instead imagines that the repulsion between ions with unlike charges is zero until they touch and is then infinite. This turns out to be a poor approximation and equation (5) leads to lattice energies which are at least 10% greater than experimentally determined values.
A better treatment uses a repulsive force which is small at large separations but rises sharply when the ions come into contact. A possible function with this behaviour is B/rn where n is large and both n and B are constants for each compound and can, in principle, be determined from measuring the compressibility of the crystal. The resulting lattice energy is the sum of the attractive term in equation (5) and this repulsive function:
|
| (6) |
At the equilibrium interatomic separation, req, Eelectrostatic is minimized and:
|
| = 0. |
|
| (7) |
Substituting this into equation (6) gives the Born-Landé equation:
|
| (8) |
The n value can be obtained from compressibility measurements and usually lies between 5 and 12. For ions with noble gas configurations, a reasonably accurate value for n can be obtained by taking the weighted average of the empirical constants in the table below.
Table 2. Approximate compressibility factors, n, for ions.
|
For example, Na+ and Mg2+ both have the same configuration as Ne and Cl- has the same configuration as Ar. The n values for NaCl and MgCl2 are thus:
NaCl: n = | and | MgCl2: n = |
More recently, the repulsive part has been represented by the function:
|
|
Use of this function yields the Born-Meyer equation:
|
| (9) |
The table below compares the experimental lattice energy for NaCl with that obtained using the hard-sphere model (equation (5)), the Born-Landé model (equation (8)) and the Born-Meyer model (equation (9)).
Table 3. Comparison of the experimental and calculated lattice energy for NaCl.
|
||||||||||||||||||||
The hard-sphere, Born-Landé and Born-Meyer equations unfortunately require knowledge of the Madelung constant and hence the crystal structure. They therefore cannot be used to predict stabilities of unknown compounds. The Born-Landé and Born-Meyer equations also require knowledge of the compressibility variables, n and ρ respectively.
Kapustinskii noticed that the Madelung constant divided by the number of ions in the chemical formula, v, is almost constant for many crystal structures. Table 1 includes the value of A/v for various MX (v = 1), MX2 (v = 3) and M2X (v = 3) structures. It varies between 0.73 – 0.88. Kapustinskii also proposed using a universal value of ρ = 0.345 and sums of tabulated values of cation (r+) and anion (r- radii in place of the measured value of their separation in the structure. The result of these simplifications is, with all constants in SI units, the Kapustinskii equation:
|
| (10) |
As shown in Table 3, the Kapustinskii equation yields lattice energies which are very similar to those obtained using the more accurate equations. It has the distinct advantage that all it requires is knowledge of the chemical formula of the ionic compound.
You will need to use this in the pre-lab quiz.
3 Which Crystal Structure Type Is Adopted?
In this experiment, you will investigate the simple relationships between many different crystal structures. The question remains, however, which one will be adopted by any given compound? One simple factor is the stoichiometry of the compound – the ratio of the number of cations to anions is controlled by the need for the whole structure to be electrically neutral.
As noted above, for any given stoichiometry, the Madelung constant and hence the lattice energy increases with the coordination number of the cation and anion. This is the reason why higher coordination numbers are always favoured. However, as the coordination number around the cation increases, it becomes increasingly difficult to maintain cation-anion contact without the anions overlapping. This is the basis of the radius ratio rules.
| ||||||||||||||||||||||||||||||
4 Do The Radius Ratio Rules Work?
The figure below shows the actual structures adopted by the alkali metal halides – a set that must be considered the most ionic of all compounds. As can be seen, although the rules predict a spread of 4, 6, 8 and even 12-coordinate structures, all of the compounds except CsCl, CsBr and CsI actually adopt the rocksalt structure! The three exceptions have the CsCl structure. Clearly, the radius ratio rules should be used with extreme care.
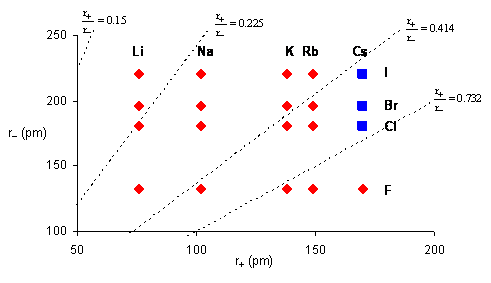 |
Figure 6. The relationship between the structures of the alkali metal halides (u NaCl and n CsCl) and ionic radii. The dotted lines showing the limiting radius ratios for 3, 4, 6 and 8 coordination.