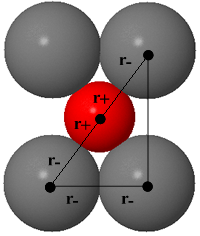
The rotatable structure opposite shows the CsCl structure in which the Cs+ ion is surrounded by 8 Cl- ions. To get as close to the cation as possible, the anions must touch along the edge of the cube, as shown in the figure below. Click the 'Directions In Which Anions Touch' button to see this view. The side of the cube has a length, a, where: a = 2r- Along the body diagonal, the Cs+ is touching the two Cl- ions on either end so its length, d, is: d = r- + 2r+ + r- = 2r+ + 2r-

Caesium Chloride Cubic structure containing cations cubically surrounded by eight anions (and vice versa):

Figure 1 Two dimensional view of packing around Cs+ in CsCl showing two opposite edges of the unit cell.

d² = a² + a² + a² = 3a² = 3 × 4r_-² = 12r_-²

d = 2(3)^1/2r_-

2r_- + 2r₊ = 2r(3)^1/2r_-

r₊ / r_- = (3)^1/2 – 1 = 0.732

Limiting radius ratio for 6-coordination (sodium chloride structure)

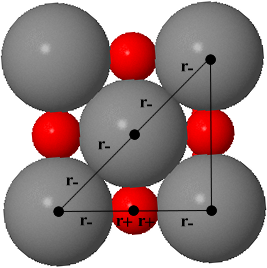
The rotatable structure opposite shows the NaCl structure in which the Na+ ion is surrounded by 6 Cl- ions. As shown in the figure below, along the cube edge, the Na+ is touching two Cl- ions so its length, a, is: a = r- + 2r+ + r- = 2r+ + 2r- To get as close to the cation as possible, the anions must touch along the diagonal of a face of the cube. Click the 'Directions In Which Anions Touch' button to see this view. The diagonal has length, d, where: d = r- + 2r- + r- = 4r-

Sodium Chloride Cubic structure containing cations cubically surrounded by six anions (and vice versa):

Figure 2 Two dimensional view of packing around Na+ in NaCl showing the face of the unit cell.

Using Pythagoras’ theorem, the length of the side and face diagonal of a cube are related:

d² = a² + a² = 2a²

d = (2)^1/2a

So,

4r_- = (2)^1/2(2r₊ + 2r_-)

r₊ / r_- = (2)^1/2 – 1 = 0.414

As long as the radius of the cation is no smaller than 41% that of the anion, the NaCl structure is possible. If the cation is larger than this, the structure is stable as the anions do not need to touch but the CsCl structure is even more stable when the cation radius reaches 73% that of the anion. If the cation radius is smaller than 41% that of the anion, the cation and anion will not be in contact. An even lower coordination number is then needed.

Limiting radius ratio for 4-coordination (zinc blende structure)

---

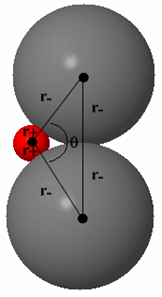
The rotatable structure opposite shows the ZnS (zinc blende) structure in which the Zn2+ ion is surrounded by 4 S2- ions. The distance from the centre of the tetrahedron to the corner, d, is: d = r+ + r- To get as close to the cation as possible, the anions must touch along the edge of the tetrahedron. Click the 'Directions In Which Anions Touch' button to see this view. This distance, a, is a = r- + r- = 2r-

Zinc Blende Cubic structure containing cations tetrahedrally surrounded by four anions (and vice versa):

Figure 3 Two dimensional view of packing around Zn2+ in ZnS showing half of the face diagonal of the unit cell.

The tetrahedral angle, q, is 109.5° so

sin(q/2) = r_- / (r₊ + r_-)

So,

sin(54.7°) = r_- / (r₊ + r_-)

r₊ / r_- = 0.225

As long as the radius of the cation is no smaller than 23% that of the anion, the ZnS structure is possible. If the cation is larger than this, the structure is stable as the anions do not need to touch but the NaCl structure is even more stable when the cation radius reaches 41% that of the anion.

Back to E12