Half-Cell Potentials
If a cell is constructed from two half-cells, and a voltmeter included in the conducting wire, then the observed potential difference is a measure of the difference in reducing power of the two couples. In this way, the reducing power of a particular couple can be specified as the potential of its half-cell relative to another half-cell. This can only ever be a relative measure as it is not possible to measure the potential of a half-cell in isolation.
By choosing a particular half-cell (couple) as a reference standard, the reducing power of any other half-cell can be specified as a particular potential. For this purpose the reference standard chosen is the standard hydrogen half-cell . This consists of the couple H+ (aq)/H2(g) (with platinised platinum as the solid conductor), the pressure of H2(g) being 101 kPa exactly, and the concentration of H+(aq) being 1 M exactly. The potential of this half-cell is then defined as zero at all temperatures. If any other half-cell is connected to this reference half-cell, the observed potential difference between them is then a measure of the electrode potential, E , of the half-cell under test. If the components of this half-cell also have concentrations of 1 M exactly for a solute and pressure equal to 101 kPa exactly for a gas, then the potential difference is defined as the standard electrode-potential , Eo. This is also sometimes called the reduction potential.
The potential difference of the cell composed of the Pt / H+ / H2 and Cu2+ / Cu couples (all components in their standard states) is 0.34 volt and the copper half-cell is positive with respect to the hydrogen half-cell. Hence the value of Eo for the Cu2+ / Cu couple is +0.34 volt. The reaction that occurs is
H2 + Cu2+ Cu + 2H+
It is seen that the Cu2+ / Cu couple undergoes reduction while the Pt / H+ / H 2 couple undergoes oxidation.
The potential difference of the cell composed of the Pt / H+ / H2 and Zn2+ / Zn couples (all components in their standard states) is 0.76 volt and the zinc half-cell is negative with respect to the hydrogen half-cell. Hence the value of Eo for the Zn2+ /Zn couple is -0.76 volt. The reaction that occurs is
Zn + 2H2+ H2 + Zn2+
It is seen that the Zn2+ / Zn couple undergoes oxidation while the Pt / H+ / H2 couple undergoes reduction.
- Balance the numbers of all the atoms other than O and H.
- Balance O by adding H2O to either side.
- Balance H by adding H+ to either side.
- Balance the charges by adding electrons to either side.
- If basic conditions are specified: eliminate any H+ present by adding enough OH- to each side of the reaction equation to turn H+ into H2O.
Example (i)
Construct the ion/electron half-equation for the reduction of Cr2O72- to Cr3+ in the presence of H+.
- Balance Cr (ie. elements other than O or H)
The reaction is Cr(VI) to Cr(III)
The Cr atoms are balanced by doubling the Cr 3+Cr2O72- 
Cr3+
Cr2O72- 
2Cr3+ - Balance O
To balance for oxygen, 7 atoms must be added to the right-hand side of the equation. Since an ion/electron half-equation is for the oxidation or reduction of only one species (and hence for a change in oxidation number of only one atom, Cr in this case), the O atoms must have the same oxidation number as those on the left-hand side, namely -II.
It is convenient to insert these as H2O molecules.
Cr2O72- 
2Cr3+ + 7H2O - Balance H
To balance for hydrogen, 14 atoms must be added to the left-hand side. As with oxygen, the H atoms added must have the same oxidation number as those on the right-hand side, namely +I. It is convenient to insert them as H+.
14H+ + Cr2O72- 
2Cr3+ + 7H2O - Balance the charge
There is a total of 12 positive charges on the left side of the equation and 6 positive charges on the right. In order to balance charges, we add electrons (which have a charge of -1). Thus, if we add 6 electrons to the left side, the charges become balanced (both +6).
Note, the purpose of balancing charges is not to make both sides of the equation zero!
14 H+ + Cr2O72- + 6e- 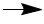
2Cr3+ + 7H2O
Note that acidic conditions were specified, so the balanced half-equation for the reduction of Cr(VI) to Cr(III) is
14 H+ + Cr2O72- + 6e- 2Cr3+ + 7H2O
Example (ii)
Construct the ion/electron half-equation for the oxidation of Ag to Ag2S through reaction with HS- in the presence of OH-.
- Balance Ag and S (ie. elements other than O or H)
The reaction is Ag(0) to Ag(I). Sulfur remains at -II.
The Ag atoms are balanced by doubling the AgAg + HS- 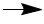
Ag2S
The S atoms are already balanced.2Ag + HS- 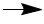
Ag2S
- Balance O
There is no oxygen present in this example to balance.2Ag + HS- 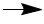
Ag2S - Balance H
To balance for hydrogen, add sufficient H+ . In our example, this requires the addition of one H+ to the right-side of the equation.2Ag + HS- 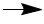
Ag2S + H+ - Balance the charge
There is a total of 1 negative charge on the left side of the equation and 1 positive charge on the right. In order to balance charges, we need to add 2 electrons to the right side.
Note that basic conditions were specified, so we need to complete Step 5 as well so as to remove any acid present.2Ag + HS- 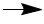
Ag2S + H+ + 2e-
- Basic conditions
There is 1 H+ present in our current equation. To eliminate this we need to add sufficient OH- to both sides of the equation so that the H+ will be neutralised.2Ag + HS- + OH- 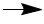
Ag2S + H+ + OH- + 2e-
This can be simplified to:
If water molecules had existed on the left-side of the equation, we could further simplify by cancelling out water molecules.2Ag + HS- + OH- 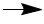
Ag2S + H2O + 2e-
2Ag + HS- + OH- Ag2S + H2O + 2e-
Alternative Method
Note that there is an alternative method for handling basic conditions that is given in some textbooks. This involves a different set of steps as outlined below:
- Balance the numbers of all the atoms other than O and H.
- Balance O by adding H2O to either side.
- Balance H by adding H2O to the side deficient in H and an equal amount of OH- to the other side.
- Balance the charges by adding electrons to either side.